
A Brief Intro to Bayesian Inference for Accounting Research
Harm Schütt, Tilburg University
2023-10-05
Photo by Riho Kroll
Part 1
Why learn something about Bayesian Statistics?
What is Bayesian statistics?
What is it useful for?
What is Bayesian statistics? (oversimplified)
Frequentist: \(P(Data|Hypothesis)\)
Bayesian: \(P(Hypothesis|Data)\)
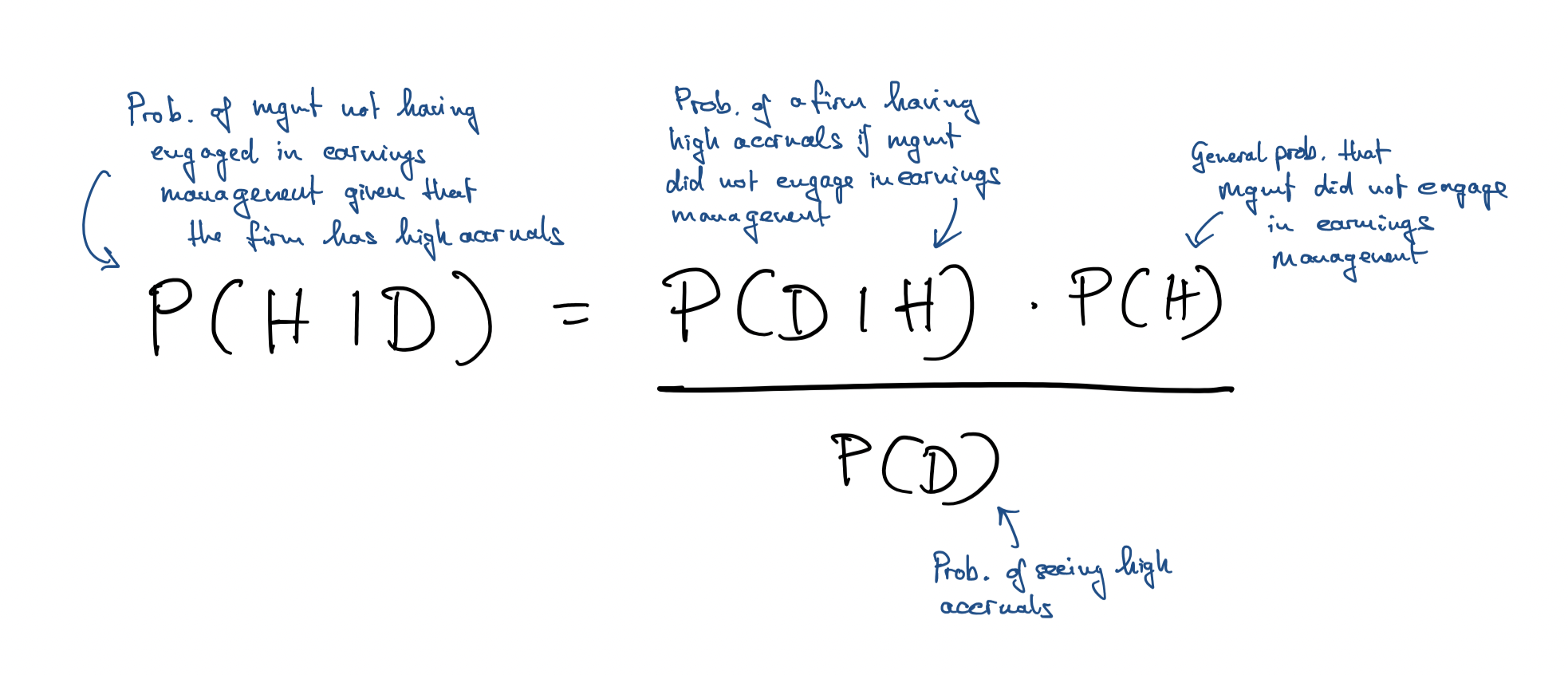
\(P(H | D) = (P(D|H) * P(H)) / P(D)\) means updating
Example: Number of successful investments \(y \sim Binom(y|N,\theta)\)
Why learn a bit of Bayesian statistics?
Photo by Erik Mclean

Not because of the philosophical differences!
To better understand frequentist statistics
To add another tool to our workbench:
- Sometimes the data is not informative enough
- Priors and DGP helps encode additional information/assumptions
- Useful for constructing finer measures and measuring latent constructs
Example: Precise firm-level measures
\[R_{i,t} = a_i + b_i * X_{i,t} + u_{i,t}\]

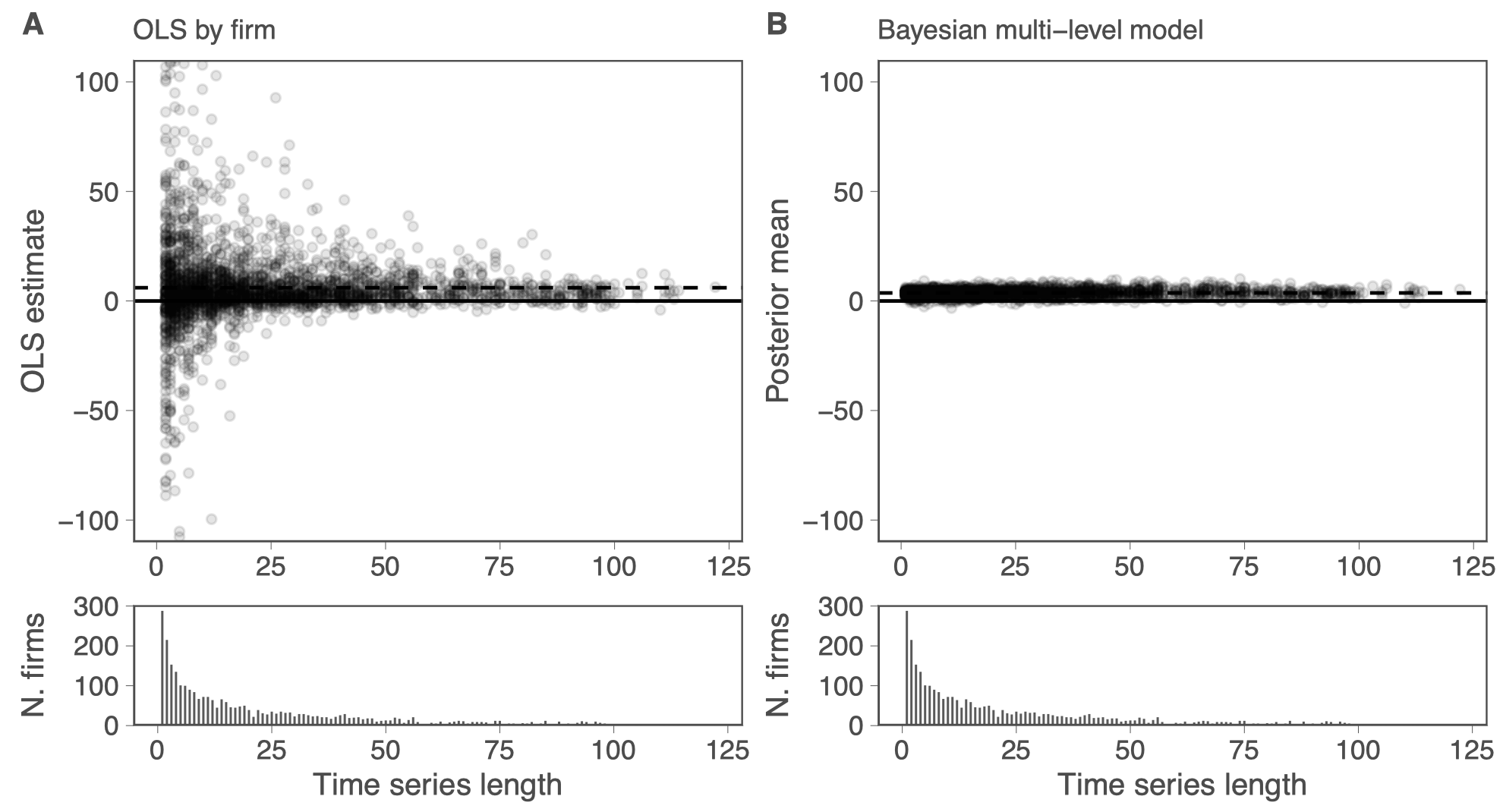
Cross-learning the prior. Helps discipline noisy estimates
Example: Modeling uncertainty


When we do not trust our models we should average. Increases power and reduce false positives in tests for opportunistic earnings management
Example: Modelling hidden dynamics (1)

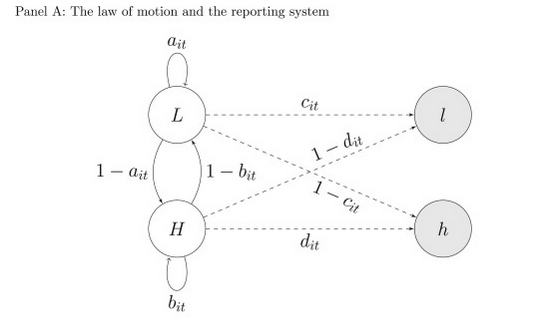
How well do earnings reveal an unobserved true state of the firm?
Example: Modelling hidden dynamics (2)

Disclosures become more (less) frequent when investors’perception of the firm is worse (better) than the true profitability
Summary: Where does Bayes help?
- Modeling heterogeneity. E.g., firm-level measures
- Modeling uncertainty
- Modeling latent constructs
Modeling a data-generating-process (incl. priors) allows us to include more information/assumptions into our analysis
Part 2
The Frequentist Baseline
Data is random. The logic behind hypothesis tests.
The importance of test power
Overfitting is a serious issue
Some simulated datasets
- Simulate 50 samples from: \(y = 1 + 2 \times x + u,\ u\sim N(0, 20)\).
- \(x\) is only drawn once (not 50 times) from: \(x \sim N(0,1)\).
Estimates vary across samples
\[y = a_0 + a_1 \times x + u\]
# A tibble: 50 × 5
id a0 a1 plabs first_sample
<int> <dbl> <dbl> <chr> <fct>
1 1 0.760 4.38 (0.8,4.4) 1
2 2 1.76 -0.0400 (1.8,0) 0
3 3 6.46 0.738 (6.5,0.7) 0
4 4 3.20 0.561 (3.2,0.6) 0
5 5 0.328 5.24 (0.3,5.2) 0
6 6 0.786 6.17 (0.8,6.2) 0
7 7 -0.877 -1.58 (-0.9,-1.6) 0
8 8 2.18 -3.30 (2.2,-3.3) 0
9 9 -0.345 1.00 (-0.3,1) 0
10 10 -0.545 3.49 (-0.5,3.5) 0
# ℹ 40 more rows- Where is the variation in \(a_0\), \(a_1\) coming from?
- Why? What are we trying to simulate?
Unmeasured influences cause estimates to vary
\[y = 1 + 2 \times x + u ,\ u \sim N(0, 20),\ x\sim N(0,1)\]
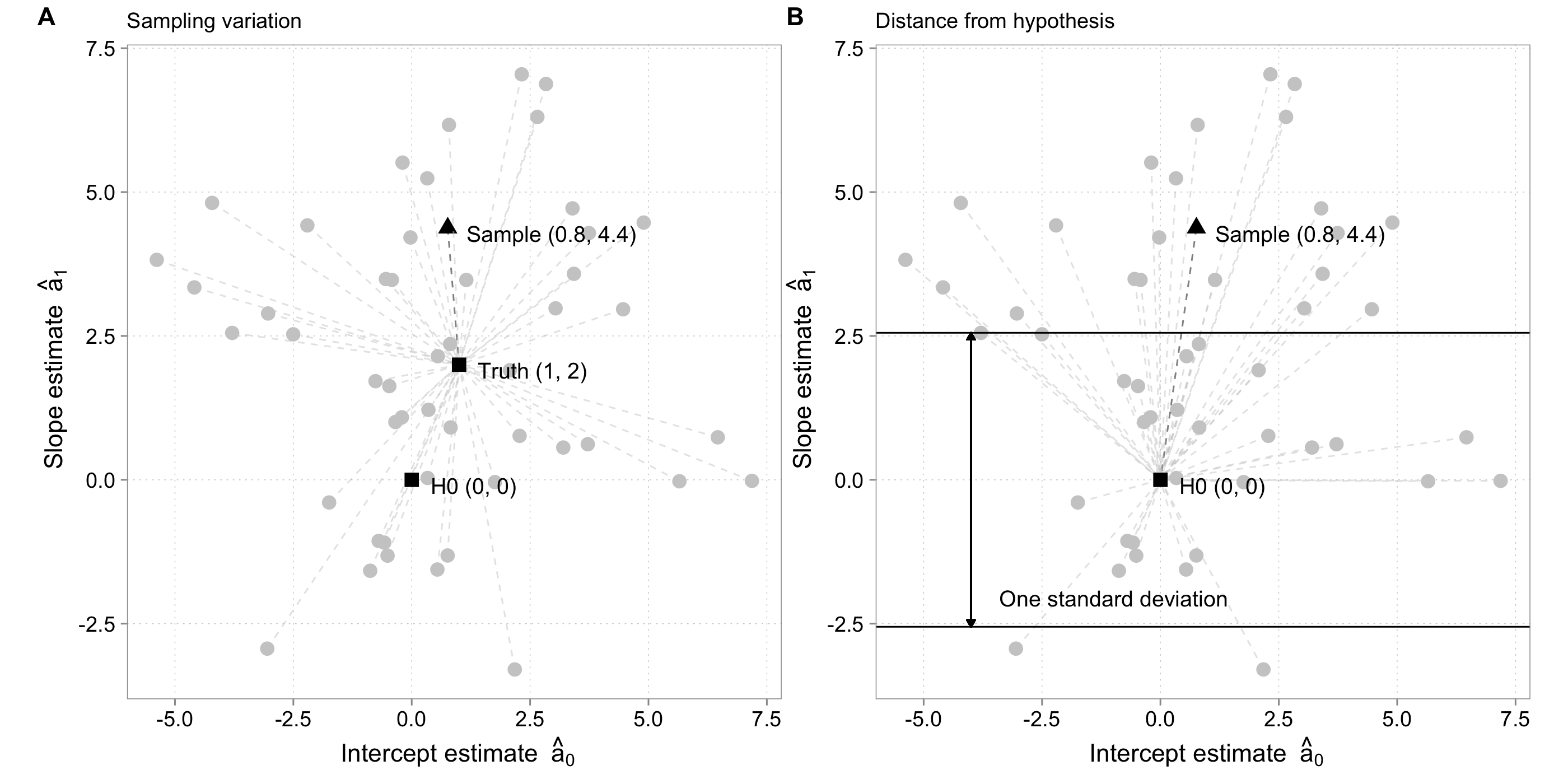
Hypothesis tests judge the data’s distance from \(H_0\)
Test logic:
- Compute a “normalized distance” from \(H_0\) using S.E.
- Figure out what distribution describes distance (assumptions)
- Pick a threshold. When is an estimate considered too distant?
- Too distant means: Unlikely to be generated under \(H_0\)
Normalization: S.E. depends on assumed behavior of unmeasured determinants (\(u\)) and \(N\)

Be careful interpreting coefficient magnitudes in low power situations
- Coefficients very large for those intervals that do not include zero
- Gets worse with less power (unexplained variance vs. N obs)
- “That which does not destroy my statistical significance makes it stronger” fallacy
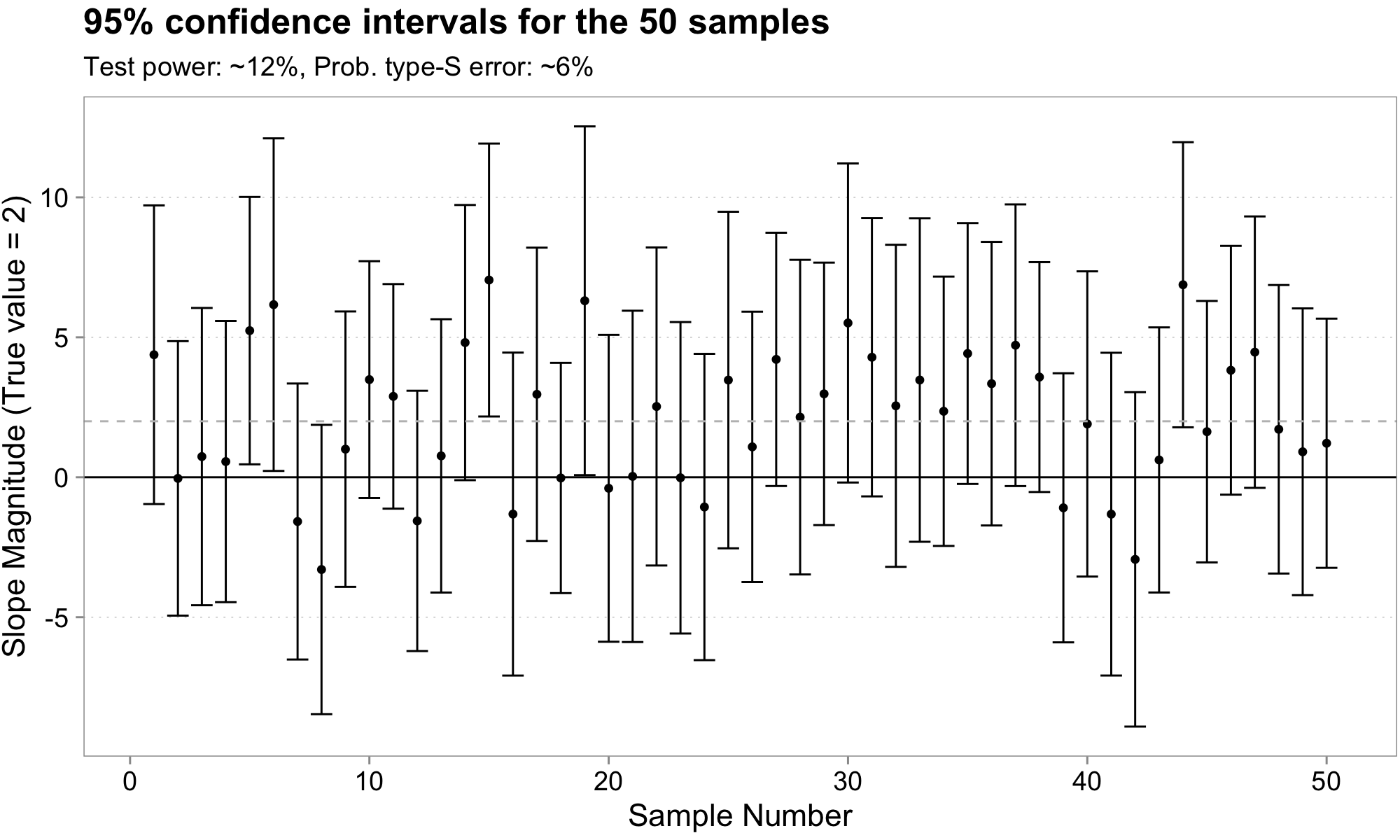
But my N is > 200.000 obs. Power is not an issue
Well … Let’s remember this picture

Effective N goes down quickly once we want to estimate heterogeneity in something we care about
And then there is overfitting…
Drawing 5 samples from \(y \sim N(-200 + 10 * x, (x+30)^2\)

Overfitting means we fitted sample idiosyncrasies
| Sample | In-Sample MSE Difference | Avg. Out-of-Sample MSE Difference |
|---|---|---|
| 1 | -8.5 | -15.1 |
| 2 | -1419.8 | 1770.0 |
| 3 | -778.7 | 901.7 |
| 4 | -2735.2 | 4602.0 |
| 5 | -8.4 | -15.1 |
Summary: Frequentist Statistics is great, but:
- Right model: Significant estimates in low power situations are often way off
- Model uncertainty: Overfitting can occur quite quickly
When we model heterogeneity or use complicated models, both issues become very important. Need to be dealt with.
Part 3
Using Bayesian inference to discipline the data
Priors regularize, which combats overfitting and extreme estimates
Priors can be learned from data
A lot of extra information can be flexibly modeled
A simple Bayesian regression
First we define the DGP:
Likelihood \(P(D | H)\):
\[y = a_0 + a_1 * x + \epsilon, \,\,\,\, \epsilon \sim N(0, \sigma)\]
Coefficient priors \(P(a_k)\):
\[a_k \sim N(0, 100), \,\,\,k \in (0, 1)\]
Residual variance prior \(P(\sigma)\):
\[\sigma \sim Exponential(\frac{1}{21})\]
No additional information in the DGP
We basically get the same inference as with classic OLS

Imagine theory suggests that \(a_1\) cannot be large
Likelihood \(P(D | H)\):
\[y = a_0 + a_1 * x + \epsilon, \,\,\,\, \epsilon \sim N(0, \sigma)\]
Coefficient priors \(P(a_k)\):
\[a_0 \sim N(0, 100)\]
\[a_1 \sim N(0, 4)\]
Residual variance prior \(P(\sigma)\):
\[\sigma \sim Exponential(\frac{1}{21})\]
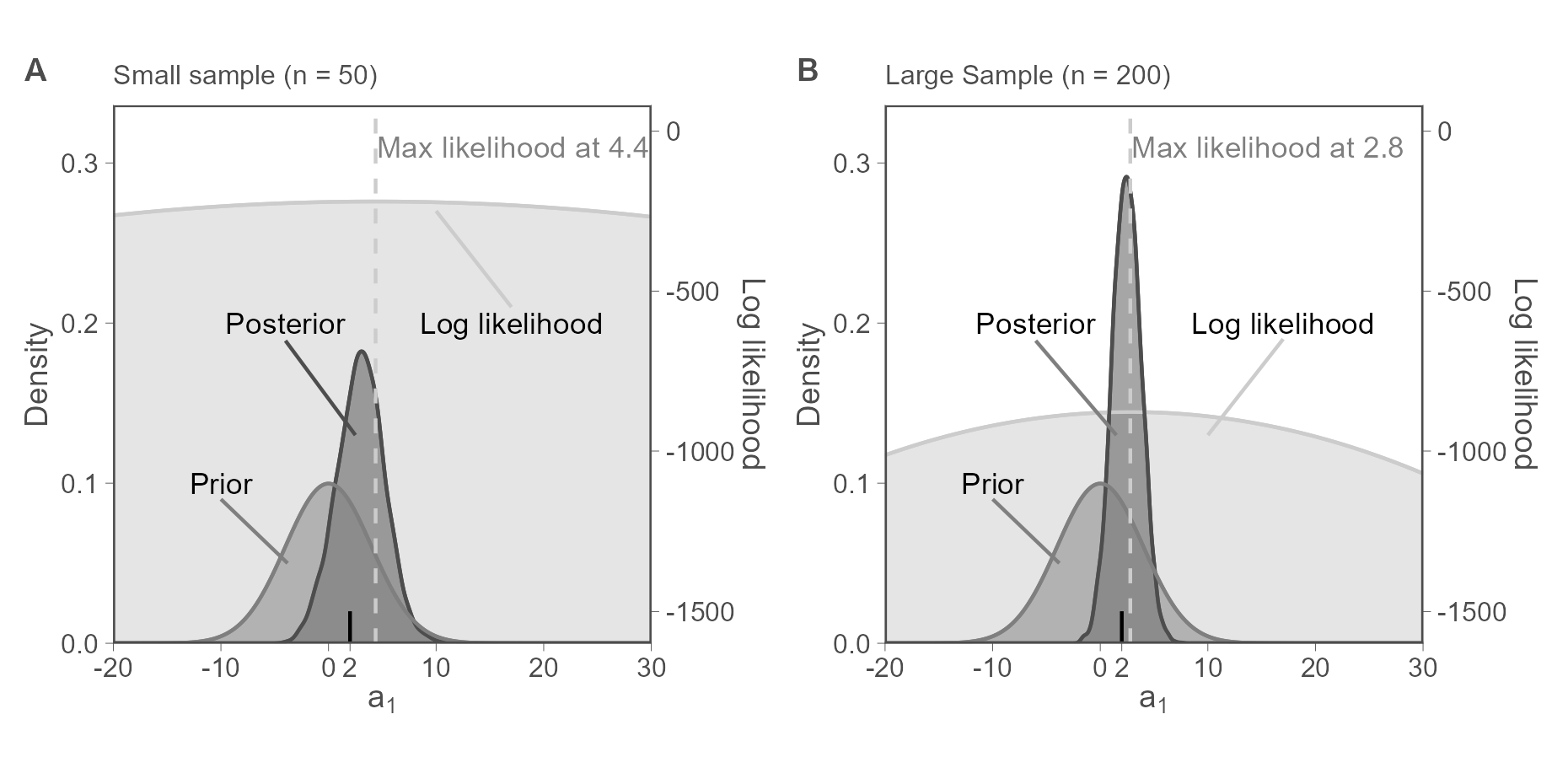
A weakly informative prior disciplines the model
Our posterior beliefs about \(a_1\) have moved closer to the truth.

Posteriors are bascially a weighted average of the likelihood and the prior
Assume \(y\sim N(\mu, \sigma^2)\) with known sigma and a prior for \(\mu \sim N(\mu_0, \sigma_0^2)\)
Then the posterior is a weighted average of the form:
\[P(\mu | y) \sim N\left(\frac{1}{\frac{1}{\sigma^2_0} + \frac{n}{\sigma^2}} * \left(\frac{1}{\sigma^2_0}*\mu_0 + \frac{n}{\sigma^2}*\frac{\sum^n y}{n}\right), \frac{1}{\frac{1}{\sigma^2_0} + \frac{n}{\sigma^2}}\right)\]
Priors have little weight when data is informative
An implication of the weighted average formula
Priors help variable selection (think Lasso)
Especially relevant when:
- Variables are noisy proxies
- Variables are correlated (including interactions)
If we can assume that only a few covariates are effectively non-zero, we want sparse priors

Priors can be learned from the data
We can estimate priors, assuming that units come from the same distribution
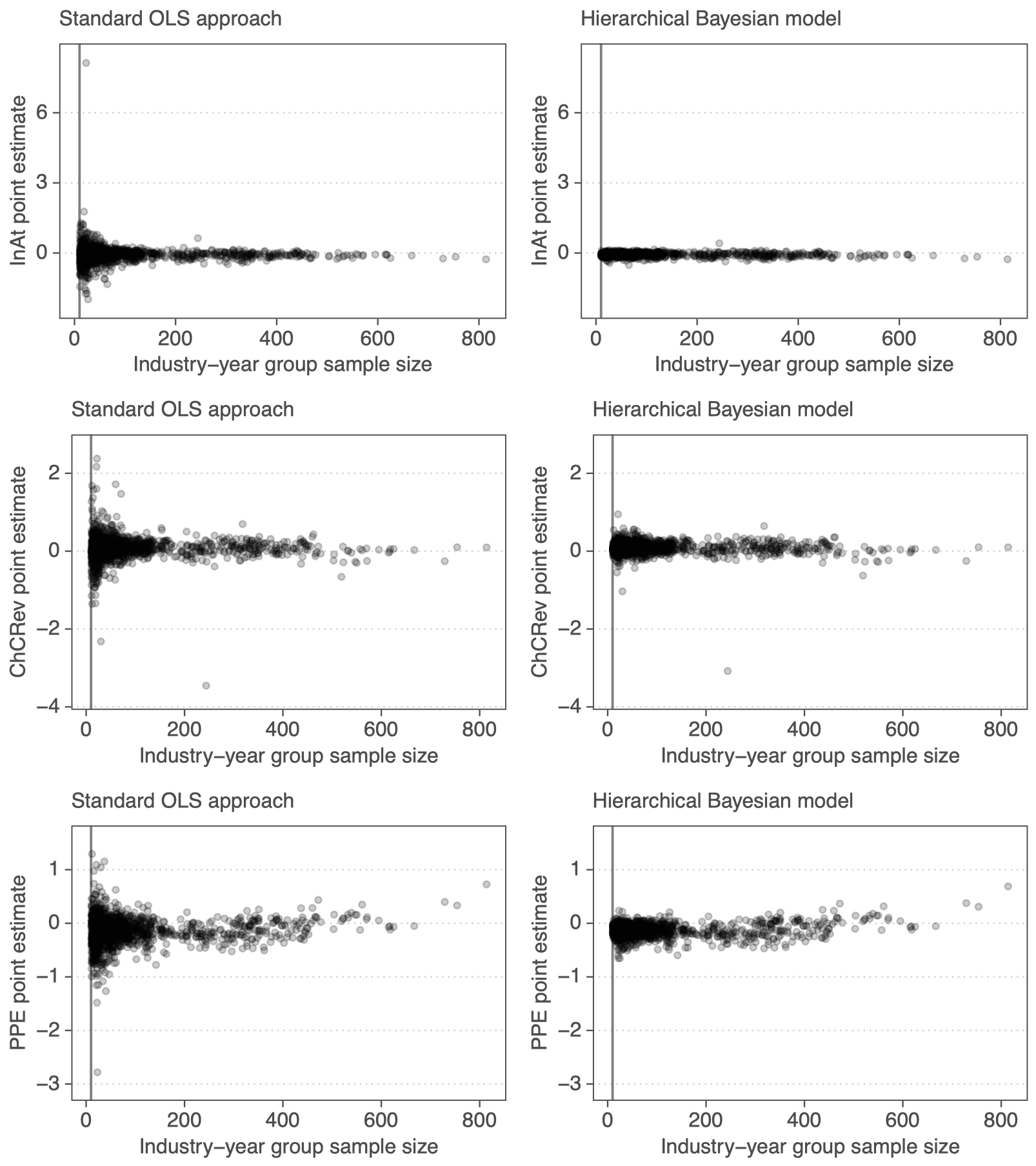
\[ \begin{align} TA_{ijt} & = \beta_{0,jt}InvAt_{ijt-1} + \beta_{1,jt}\triangle CRev_{ijt}\\\nonumber & + \beta_{2,jt}PPE_{ijt} \end{align} \]
Priors:
\[ \begin{eqnarray} \label{eq:priors} \begin{pmatrix} \beta_{0,j,t}\\ \beta_{1,j,t}\\ \beta_{2,j,t} \end{pmatrix} & \sim & N\left(\left(\begin{array}{c} \mu_0\\ \mu_1 \\ \mu_2 \end{array}\right),\left(\begin{array}{ccc} \sigma_{0} & \rho_{0,1} & \rho_{0,2} \\ \rho_{0,1} & \sigma_1 & \rho_{1,2} \\ \rho_{0,2} & \rho_{1,2} & \sigma_2 \end{array}\right)\right) \quad \forall j,t \end{eqnarray} \] Hyper-priors:
\[ \begin{align} \mu_d & \sim N\left(0, 2.5\right) \quad \sigma_d \sim Exp\left(1\right) \quad \forall d \nonumber \\ \rho & \sim LKJcorr(2) \end{align} \]
We want regularized measures + their uncertainty
Measurement error has serious consequences for our inferences

Priors can identify latent variables
We want to estimate newspaper slant. Assume that one needs room for interpretation to slant news:
\[ \begin{align} \textit{NrNegWords}_{i, j} & \sim \text{Binom}(N_{words}, p_{neg, i, j})\\ \nonumber \text{logit}(p_{neg, i, j}) & = \textit{RoomInt}_{j} \times {OutlNeg}_{i} + BadNews_{j} \end{align} \]
Model is not identified because: \(Room_j \times Outl_i = c*Room_j \times Outl_i/c\)
Priors (non-negative \(RoomInt\) + prior scale for \(Outl\)) identify it:
\[ \begin{eqnarray} \begin{pmatrix}log(Room_j)\\ News_j \end{pmatrix} & \sim & N\left(\left(\begin{array}{c} \mu_{LRoom}\\ \mu_{News} \end{array}\right),\left(\begin{array}{cc} \sigma_{LRoom} & \rho \\ \rho & \sigma_{News} \end{array}\right)\right)\\ \nonumber Outl_i & \sim & N(0, 1) \end{eqnarray} \]
Summary: Bayesian statistics is a useful tool because
- Priors regularize, which combats overfitting and extreme estimates
- Priors can be learned from data
- A lot of extra information can be flexibly modeled
Bayesian statistics is not the only way to do all this. It’s advantage lies in its flexibility and in giving us powerful uncertainty measures for free.
Thank you for your attention
Next up: coding practice ;)