Simulation: Classical vs. Bayesian Regression

Code for the Section 2: Bayesian inference compared to classical inference

Harm Schuett https://hschuett.github.io/ (Tilburg University)https://www.tilburguniversity.edu
2021-10-04 
library(tidyverse)
library(broom)
library(patchwork)
library(cmdstanr)
source("../R/00-utils.R")
kable <- knitr::kable
theme_set(theme_prodgray())

1. Introduction and preliminaries

This markdown file contains all the code necessary to replicate the figures, models and results used in Section 2: Bayesian inference compared to classical inference of the Paper What Can Bayesian Inference Do for Accounting Research?. All the code can also be found in the repo. It contains 00-utils.R which contains a few helper functions for graphs and tables.

Note: I started using the newer cmdstanr package instead of the older rstan package because it likely is the future of the R based Stan ecosystem. I also really like its api, which is very close to the api of the pystan package. An additional advantage (I hope) is thus that most model fitting code should be more or less directly transferable to pystan for those that want to work in python.

Installing cmdstanr used to be tricky at times because one needs a working c++ toolchain. But it is much smoother now. Please see the cmdstanr doc for installation instructions

2. Creating the simulated data

First we create the 50 samples of 50 observations each

set.seed(888)
n_samples <- 50
n_obs <- 50
x_fix <- rnorm(n = n_obs, 0, 1)
gen_data <- function(n) tibble(u = rnorm(n, 0, 20), x = x_fix, y = 1 + 2 * x_fix + u)

# gen samples
samples <- tibble(id = 1:n_samples)
samples$data <- map(rep.int(n_obs, n_samples), gen_data)

Next we create the relevant figures

3. OLS regressions

3.1. OLS fits of all 50 samples

# gen ols estimates
samples$ols_fit <- map(samples$data, function(dat) tidy(lm(y ~ x, data = dat)))
ols_estimates <- samples %>%
  unnest(ols_fit) %>%
  mutate(param = if_else(term == "x", "a1", "a0")) %>%
  select(id, param, estimate) %>%
  spread(key = param, value = estimate) %>%
  mutate(
    plabs = paste0("(", round(a0, 1), ",", round(a1, 1), ")"),
    first_sample = as.factor(c(1, rep.int(0, times = n_samples - 1)))
  )

3.2. OlS estimates of the first sample

kable(samples$ols_fit[[1]])
term estimate std.error statistic p.value
(Intercept) 0.7602868 2.873058 0.2646264 0.7924303
x 4.3777130 2.653451 1.6498189 0.1055098

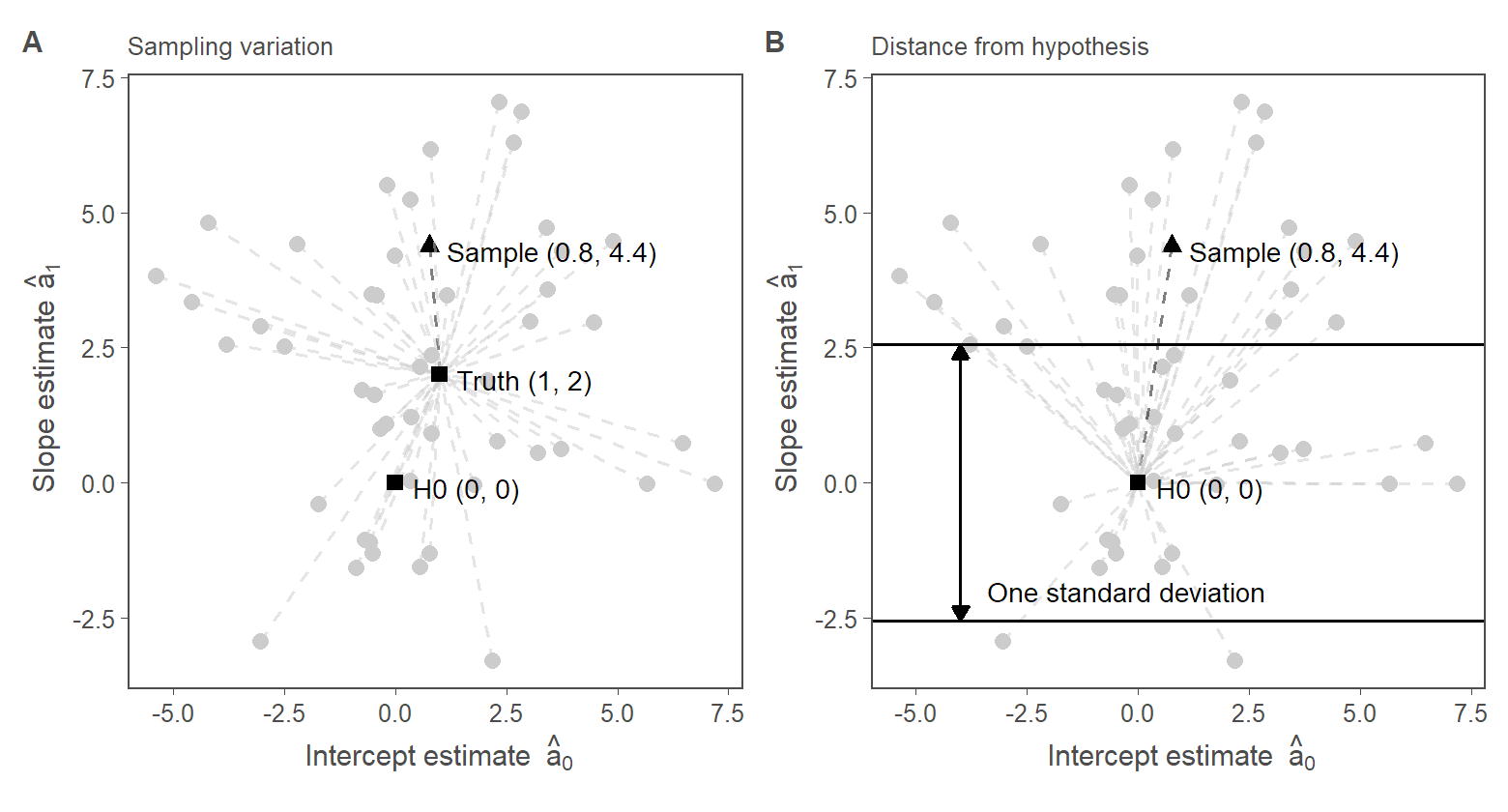
4. Fig. 1: Classical hypothesis tests

We need the following variables for scaling Fig. 1

range_x <- range(ols_estimates$a0)
range_y <- range(ols_estimates$a1)
nudge_x <- 0.1
sample_a0 <- ols_estimates$a0[1]
sample_a1 <- ols_estimates$a1[1]
r <- sd(ols_estimates$a1)

4.1. Fig.1, Panel A

f1.panA <-
  ols_estimates %>%
  ggplot(aes(x = a0, y = a1, shape = first_sample, color = first_sample)) +
  geom_point(size = 2) +
  xlim(range_x) +
  ylim(range_y) +
  scale_color_manual(values = c("gray80", "black")) +
  labs(
    x = expression(" Intercept estimate " ~ hat(a)[0]),
    y = expression(" Slope estimate " ~ hat(a)[1]),
    subtitle = "Sampling variation"
  ) +
  geom_segment(aes(color = first_sample), xend = 1, yend = 2, linetype = 2, alpha = 0.5) +
  annotate("point", x = 1, y = 2, color = "black", size = 2, shape = 15) +
  annotate("text", x = 1.4, y = 1.9, label = "Truth (1, 2)", hjust = 0, color = "black", size = 3) +
  annotate("text",
    x = sample_a0 + 0.4,
    y = sample_a1 + -0.1,
    label = paste0("Sample (", round(sample_a0, 1), ", ", round(sample_a1, 1), ")"),
    hjust = 0, color = "black", size = 3
  ) +
  annotate("point", x = 0, y = 0, color = "black", size = 2, shape = 15) +
  annotate("text", x = 0.4, y = -0.1, label = "H0 (0, 0)", hjust = 0, color = "black", size = 3) +
  theme(legend.position = "none", aspect.ratio=1)

4.2. Fig.1, Panel B

f1.panB <- 
  ols_estimates %>%
  ggplot(aes(x = a0, y = a1, shape = first_sample, color = first_sample)) +
  geom_point(size = 2) +
  xlim(range_x) +
  ylim(range_y) +
  scale_color_manual(values = c("gray80", "black")) +
  labs(
    x = expression(" Intercept estimate " ~ hat(a)[0]),
    y = expression(" Slope estimate " ~ hat(a)[1]),
    subtitle = "Distance from hypothesis"
  ) +
  theme(legend.position = "none") +
  geom_segment(aes(color = first_sample), xend = 0, yend = 0, linetype = 2, alpha = 0.5) +
  annotate("point", x = 0, y = 0, color = "black", size = 2, shape = 15) +
  annotate("text", x = 0.4, y = -0.1, label = "H0 (0, 0)", hjust = 0, color = "black", size = 3) +
  annotate("text",
    x = sample_a0 + 0.4,
    y = sample_a1 + -0.1,
    label = paste0("Sample (", round(sample_a0, 1), ", ", round(sample_a1, 1), ")"),
    hjust = 0, color = "black", size = 3
  ) +
  geom_hline(yintercept = c(r, -r), color = "black") +
  geom_segment(
    x = -4, xend = -4, y = -r, yend = r, color = "black",
    arrow = arrow(length = unit(0.07, "inches"), ends = "both", type = "closed")
  ) +
  annotate("text",
    x = -3.4, y = -2.2,
    size = 3, hjust = 0, vjust = 0, color = "black",
    label = "One standard deviation"
  ) +
  theme(legend.position = "none", aspect.ratio=1)

Saving figure

fig1 <- f1.panA + f1.panB + plot_annotation(tag_levels = "A")
save_fig(fig1, figname = "fig1", w = 6.2, h = 3.3)

fig1

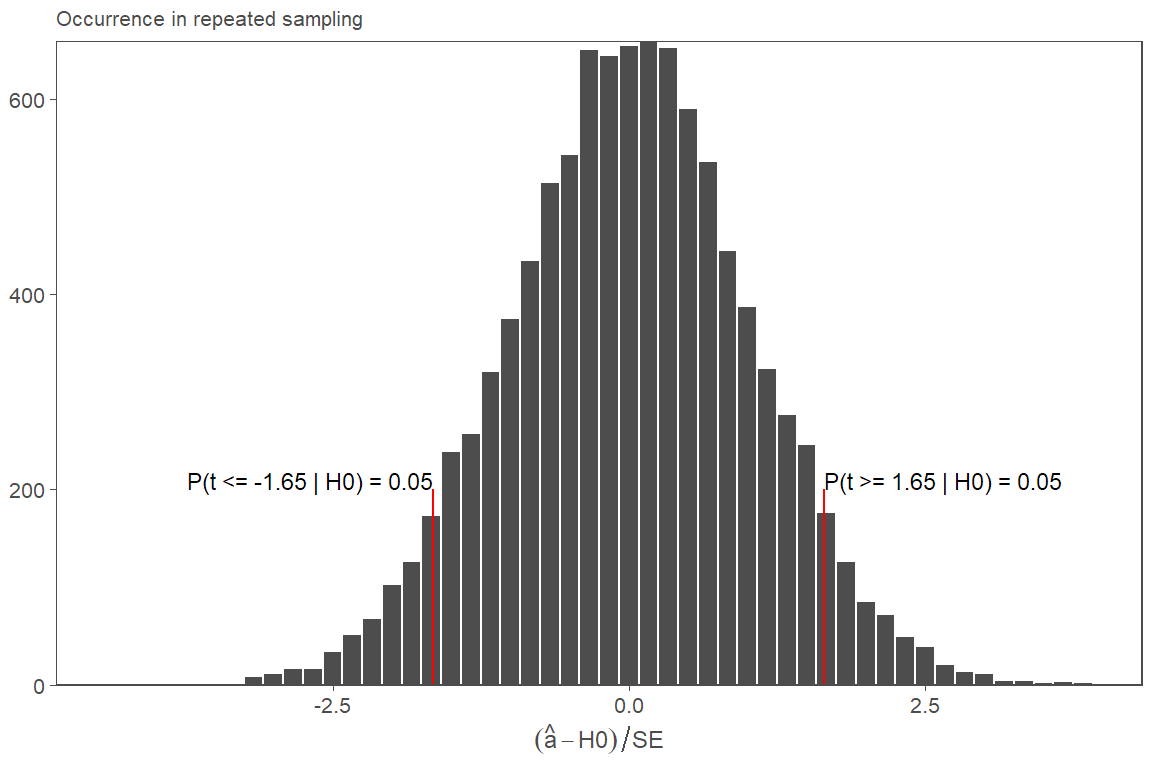
5. Additional t-test figure

This one is not in the paper. I used it for an internal Ph.D. seminar

t_dist <- data.frame(ps = rt(n=10000, df=n_obs-2))
test_stat <- 1.65
quant_test <- round(1 - pt(test_stat, df=n_obs-2), 2)

fZ <- 
  ggplot(data=t_dist, aes(x=ps)) +
  geom_histogram(bins=50, color="white", fill="gray30") +
  geom_segment(color="red",
               x=test_stat, y=0,
               xend=test_stat, yend=200) +
  geom_segment(color="red",
               x=-test_stat, y=0,
               xend=-test_stat, yend=200) +
  # geom_area(color=high_red, fill=high_red, alpha=0.5) +
  annotate("text", x=test_stat, y=200,
           size=3, hjust=0, vjust=0,
           label=paste0("P(t >= ", test_stat, " | H0) = ", quant_test)) +
  annotate("text", x=-test_stat, y=200,
           size=3, hjust=1, vjust=0,
           label=paste0("P(t <= -", test_stat, " | H0) = ", quant_test)) +
  scale_y_continuous(expand=c(0,0)) +
  labs(x = expression((hat(a)-H0)/SE),
       y = NULL,
       subtitle = "Occurrence in repeated sampling") +
  theme(legend.position = "none")
fZ

6. Fitting the Bayesian models

To fit a Bayesian model I use Stan, or, more precisely, its R bindings in cmdstanr. To fit a Bayesian model, we need to:

  1. Write the corresponding model using the Stan language
  2. Compile the code into a Stan model executable (an .exe file)
  3. Make a list of data to feed into the .exe file
  4. Let the model run and generate MCMC chains (or whatever algorithm is specified)

6.1 Bayesian model with diffuse/very weak priors

sample1 <- samples$data[[1]]

The following descriptive are useful when assessing what priors to use:

sample1_descs <- c(
  u_y = mean(sample1$y),
  u_x = mean(sample1$x),
  s_y = sd(sample1$y),
  s_x = sd(sample1$x)
) 

round(sample1_descs, 3)

   u_y    u_x    s_y    s_x 
 0.499 -0.060 20.638  1.092

The model itself is coded in the Stan language. There are many excellent tutorials on Stan available online. So I won’t waste space explaining it here. For various reasons (e.g., debugging) it is customary to put the model code in a separate .stan file. All the model files can be found in the /Stan/ folder of the repo.

cat(read_lines("../Stan/sim-vweak-priors.stan"), sep = "\n")

data{
  int<lower=1> N;
  real y[N];
  real x[N];
}
parameters{
  real a0;
  real a1;
  real<lower=0> sigma;
}
model{
  vector[N] mu;
  sigma ~ exponential( 1.0 / 21.0 );
  a0 ~ normal( 0 , 100 );
  a1 ~ normal( 0 , 100 );
  for ( i in 1:N ) {
    mu[i] = a0 + a1 * x[i];
  }
  y ~ normal( mu , sigma );
}

Next, we compile the model to an .exe file

model_vweak_priors <- cmdstan_model("../Stan/sim-vweak-priors.stan")

Now, we prepare the list of data to feed into the model.

input_data <- list(
  y = sample1$y,
  x = sample1$x,
  N = nrow(sample1)
)

We run the model

fit_vweak_priors <- model_vweak_priors$sample(
  data = input_data,
  iter_sampling = 1000,
  iter_warmup = 1000,
  chains = 4,
  parallel_chains = 4,
  seed = 1234,
  refresh = 1000
)

Running MCMC with 4 parallel chains...

Chain 1 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 1 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 1 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 1 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 2 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 2 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 2 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 2 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 3 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 3 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 3 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 4 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 1 finished in 0.1 seconds.
Chain 2 finished in 0.1 seconds.
Chain 3 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 3 finished in 0.1 seconds.
Chain 4 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 4 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 4 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 4 finished in 0.1 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.6 seconds.

Here is the summary of the resulting posterior distribution of the model parameters

fit_vweak_priors$summary(variables = c("sigma", "a0", "a1")) |> 
  mutate(across(where(is.numeric), round, 3)) |> 
  kable()
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
sigma 20.556 20.380 2.125 2.074 17.446 24.220 1.003 3094.064 2515.482
a0 0.756 0.778 2.921 2.932 -3.884 5.581 1.000 3366.030 2861.077
a1 4.241 4.241 2.665 2.681 -0.186 8.541 1.000 3496.024 2752.886

Posterior descriptives

This is one form of getting the mcmc chain output. We need the draws to draw inferences about the posterior.

postdraws_vweak_prior <- fit_vweak_priors$draws(format = "draws_df")
head(postdraws_vweak_prior)

# A draws_df: 6 iterations, 1 chains, and 4 variables
  lp__     a0   a1 sigma
1 -173  2.697  4.0    21
2 -174 -1.066  6.8    18
3 -173  0.071  5.6    19
4 -174  2.678  6.5    23
5 -174 -1.515  2.1    18
6 -176 -1.275 -2.1    23
# ... hidden reserved variables {'.chain', '.iteration', '.draw'}

The posterior 90% centered credible interval:

quantile(postdraws_vweak_prior$a1, probs = c(0.05, 0.95))

        5%        95% 
-0.1861673  8.5411815

The posterior probability that a1 < 0:

emp_a1 <- ecdf(postdraws_vweak_prior$a1)
emp_a1(0)

[1] 0.05825

6.2. Bayesian model with weakly informative priors

This is basically the same model, just with different hard-coded priors.

cat(read_lines("../Stan/sim-wkinfo-priors.stan"), sep = "\n")

data{
  int<lower=1> N;
  real y[N];
  real x[N];
}
parameters{
  real a0;
  real a1;
  real<lower=0> sigma;
}
model{
  vector[N] mu;
  sigma ~ exponential( 1.0 / 21.0 );
  a0 ~ normal( 0 , 100 );
  a1 ~ normal( 0 , 4 );
  for ( i in 1:N ) {
    mu[i] = a0 + a1 * x[i];
  }
  y ~ normal( mu , sigma );
}
model_wkinfo_priors <- cmdstan_model("../Stan/sim-wkinfo-priors.stan")

Because we use the same data (The list input_data), we can fit the new model now:

fit_wkinfo_priors <- model_wkinfo_priors$sample(
  data = input_data,
  iter_sampling = 1000,
  iter_warmup = 1000,
  chains = 4,
  parallel_chains = 4,
  seed = 1234,
  refresh = 1000
)

Running MCMC with 4 parallel chains...

Chain 1 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 1 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 1 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 1 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 2 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 2 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 2 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 2 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 3 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 3 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 3 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 3 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 4 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 4 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 4 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 1 finished in 0.1 seconds.
Chain 2 finished in 0.1 seconds.
Chain 3 finished in 0.1 seconds.
Chain 4 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 4 finished in 0.1 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.3 seconds.

Here is the summary of the resulting posterior distribution of the model parameters

fit_wkinfo_priors$summary(variables = c("sigma", "a0", "a1")) |> 
  mutate(across(where(is.numeric), round, 3)) |> 
  kable()
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
sigma 20.567 20.358 2.161 2.072 17.333 24.506 1.001 4276.167 3167.417
a0 0.672 0.690 2.878 2.897 -4.040 5.364 1.000 4199.116 2467.601
a1 2.978 3.013 2.213 2.186 -0.793 6.560 1.001 4074.289 3219.891

Posterior descriptives

The posterior 90% centered credible interval:

postdraws_wkinfo_prior <- fit_wkinfo_priors$draws(format = "draws_df")
quantile(postdraws_wkinfo_prior$a1, probs = c(0.05, 0.95))

        5%        95% 
-0.7927523  6.5595845

The posterior probability that a1 < 0:

emp_a1 <- ecdf(postdraws_wkinfo_prior$a1)
emp_a1(0)

[1] 0.092

7. Fig. 2: Visualization of Bayesian inference

7.1. Data preparations

The following code generates the density estimates, for the a1 posterior panels

# helper function for panel D
get_dens <- function(ppd, probs = c(0.05, 0.95)) {
  dens <- density(ppd)
  mode3 <- dens$x[dens$y == max(dens$y)]
  mode3.den <- dens$y[dens$x == mode3]
  dens.df <- data.frame(x = dens$x, y = dens$y)
  quantiles <- quantile(ppd, prob = probs)
  dens.df$quant <- factor(findInterval(dens.df$x, quantiles))
  dens.df$Q1 <- quantiles[1]
  dens.df$Q2 <- quantiles[2]
  return(dens.df)
}

post_dens <- get_dens(postdraws_vweak_prior$a1)
post_dens2 <- get_dens(postdraws_wkinfo_prior$a1)

max_dens <- max(c(post_dens$y, post_dens2$y))

The following code generates the density estimates, for the prior panels

x_length <- seq(-300, 300, length.out = 1000)
x_length2 <- seq(0, 100, length.out = 1000)
priors <- data.frame(
  a_den = dnorm(x = x_length, mean = 0, sd = 100),
  sigma_den = dexp(x = x_length2, rate = (1/21)),
  x1 = x_length,
  x2 = x_length2
)
priors2 <- data.frame(
  a_den = dnorm(x = x_length, mean = 0, sd = 4),
  sigma_den = dexp(x = x_length2, rate = (1/21)),
  x1 = x_length,
  x2 = x_length2
)

max_dens_a_prior <- max(c(priors$a_den, priors2$a_den))

Getting the plot ranges

range_a0 <- c(
  min(min(postdraws_vweak_prior$a0), min(postdraws_vweak_prior$a0)), 
  max(max(postdraws_vweak_prior$a0), max(postdraws_vweak_prior$a0))
)
range_a1 <- c(
  min(min(postdraws_vweak_prior$a1), min(postdraws_vweak_prior$a1)), 
  max(max(postdraws_vweak_prior$a1), max(postdraws_vweak_prior$a1))
)

7.2. Fig.2, Subfigure 1

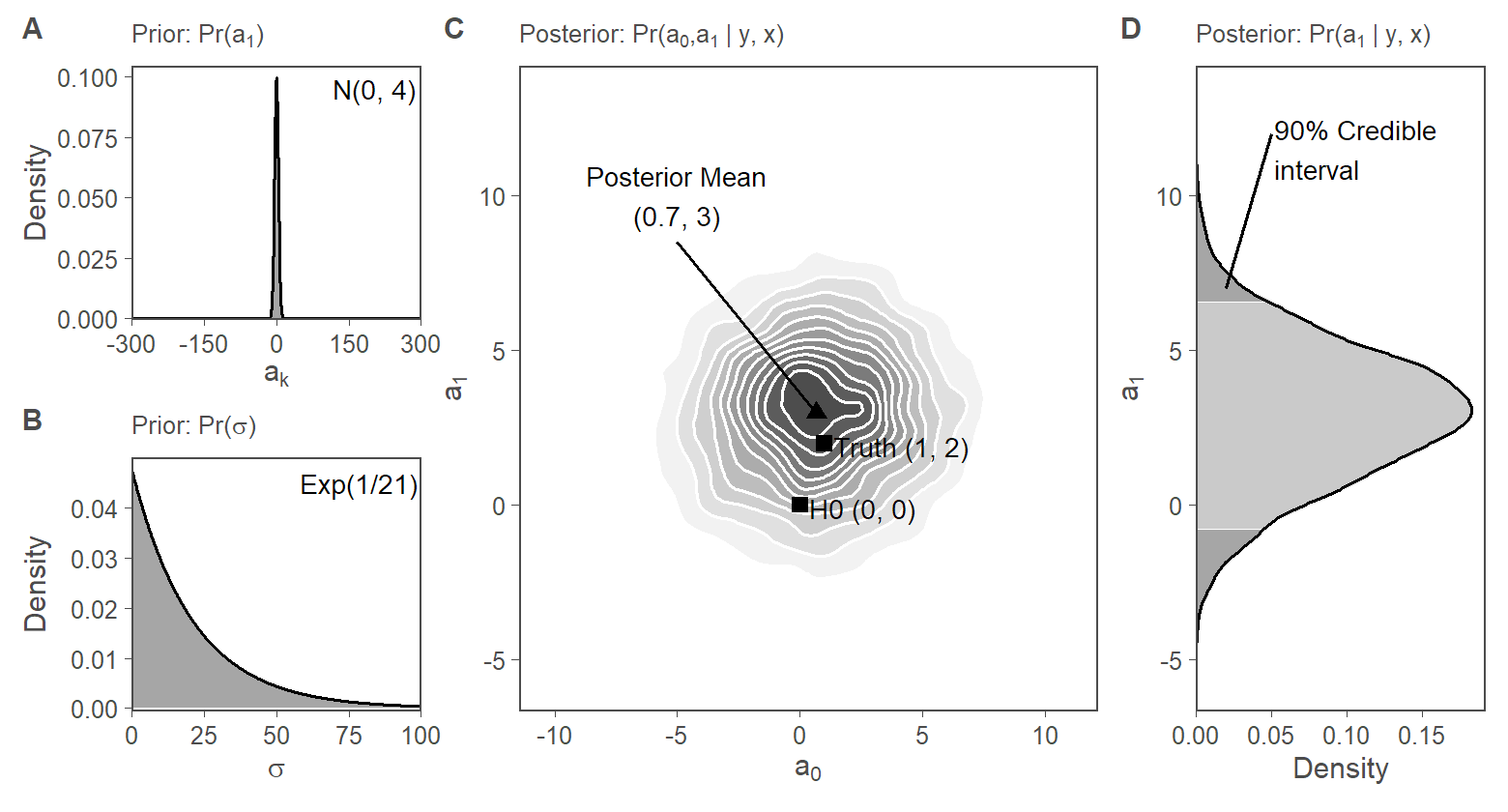
f2.s1.panC <-
  ggplot(data = postdraws_vweak_prior, aes(x = a0, y = a1)) +
  stat_density_2d(aes(fill = ..level..), geom = "polygon", colour = "white") +
  annotate("point", x = 1, y = 2, color = "black", size = 2, shape = 15) +
  annotate("text", x = 1.4, y = 1.9, label = "Truth (1, 2)", hjust = 0, color = "black", size = 3) +
  annotate("point",
    x = mean(postdraws_vweak_prior$a0), y = mean(postdraws_vweak_prior$a1),
    color = "black", size = 2, shape = 17
  ) +
  annotate("text",
    x = -5, y = 10,
    label = paste0(
      "Posterior Mean\n(",
      round(mean(postdraws_vweak_prior$a0), 1),
      ", ",
      round(mean(postdraws_vweak_prior$a1), 1),
      ")"
    ),
    hjust = 0.5, color = "black", size = 3
  ) +
  annotate("segment",
    x = mean(postdraws_vweak_prior$a0), xend = -5,
    y = mean(postdraws_vweak_prior$a1), yend = 8.5
  ) +
  annotate("point", x = 0, y = 0, color = "black", size = 2, shape = 15) +
  annotate("text", x = 0.4, y = -0.1, label = "H0 (0, 0)", hjust = 0, color = "black", size = 3) +
  scale_x_continuous(expand = c(0, 0), limits = range_a0) +
  scale_y_continuous(expand = c(0, 0), limits = range_a1) +
  scale_fill_continuous(low = "grey95", high = "grey30") +
  theme(legend.position = "none") +
  labs(
    x = expression(a[0]),
    y = expression(a[1]),
    subtitle = quote("Posterior: Pr(" * a[0] * "," * a[1] * " | y, x)")
  )
f2.s1.panA <-
  ggplot(data = priors, aes(x = x1, y = a_den)) +
  geom_area(color = "black", fill = "grey30", alpha = 0.5) +
  scale_y_continuous(expand = expansion(mult = c(0.001, 0.05)), limits = c(0, max_dens_a_prior) ) +
  annotate("text", x = 290, y = 0.095, label = "N(0, 100)", hjust = 1, color = "black", size = 3) +
  scale_x_continuous(expand = c(0, 0), breaks = c(-300, -150, 0, 150, 300)) +
  labs(
    y = "Density",
    x = expression(a[k]),
    subtitle = quote("Prior: Pr(" * a[k] * ")")
  )
f2.s1.panB <-
  ggplot(data = priors, aes(x = x2, y = sigma_den)) +
  geom_area(color = "black", fill = "grey30", alpha = 0.5) +
  scale_y_continuous(expand = expansion(mult = c(0.01, 0.05))) +
  scale_x_continuous(expand = c(0, 0)) +
  annotate("text", x = 99, y = 0.045, label = "Exp(1/21)", hjust = 1, color = "black", size = 3) +
  labs(
    y = "Density",
    x = expression(sigma),
    subtitle = quote("Prior: Pr(" * sigma * ")")
  )
f2.s1.panD <-
  post_dens %>%
  ggplot(aes(x = x)) +
  geom_ribbon(aes(ymin = 0, ymax = y, fill = quant), alpha = 0.7) +
  geom_line(aes(y = y), color = "black") +
  labs(
    x = expression(a[1]),
    y = expression("Density"),
    subtitle = quote("Posterior: Pr(" * a[1] * " | y, x)")
  ) +
  scale_x_continuous(expand = c(0, 0)) +
  scale_y_continuous(expand = expansion(mult = c(0.0, 0.05))) +
  scale_fill_manual(values = c("grey50", "grey70", "grey50")) +
  theme(legend.position = "None") +
  annotate("segment", x = 7, xend = 12, y = 0.02, yend = 0.05) +
  annotate("text", x = 11.5, y = 0.052, label = "90% Credible\ninterval", color = "black", size = 3, hjust = 0) +
  coord_flip(xlim = range_a1, ylim = c(0, max_dens))

layout <- "
ACCD
BCCD
"

fig2.s1 <- f2.s1.panA + f2.s1.panB + f2.s1.panC + f2.s1.panD +
  plot_layout(design = layout) +
  plot_annotation(tag_levels = "A")

7.3. Fig.2, Subfigure 2

f2.s2.panC <-
  ggplot(data = postdraws_wkinfo_prior, aes(x = a0, y = a1)) +
  stat_density_2d(aes(fill = ..level..), geom = "polygon", colour = "white") +
  annotate("point", x = 1, y = 2, color = "black", size = 2, shape = 15) +
  annotate("text", x = 1.4, y = 1.9, label = "Truth (1, 2)", hjust = 0, color = "black", size = 3) +
  annotate("point",
    x = mean(postdraws_wkinfo_prior$a0), y = mean(postdraws_wkinfo_prior$a1),
    color = "black", size = 2, shape = 17
  ) +
  annotate("text",
    x = -5, y = 10,
    label = paste0(
      "Posterior Mean\n(",
      round(mean(postdraws_wkinfo_prior$a0), 1),
      ", ",
      round(mean(postdraws_wkinfo_prior$a1), 1),
      ")"
    ),
    hjust = 0.5, color = "black", size = 3
  ) +
  annotate("segment",
    x = mean(postdraws_wkinfo_prior$a0), xend = -5,
    y = mean(postdraws_wkinfo_prior$a1), yend = 8.5
  ) +
  annotate("point", x = 0, y = 0, color = "black", size = 2, shape = 15) +
  annotate("text", x = 0.4, y = -0.1, label = "H0 (0, 0)", hjust = 0, color = "black", size = 3) +
  scale_x_continuous(expand = c(0, 0), limits = range_a0) +
  scale_y_continuous(expand = c(0, 0), limits = range_a1) +
  scale_fill_continuous(low = "grey95", high = "grey30") +
  theme(legend.position = "none") +
  labs(
    x = expression(a[0]),
    y = expression(a[1]),
    subtitle = quote("Posterior: Pr(" * a[0] * "," * a[1] * " | y, x)")
  )
f2.s2.panA <-
  ggplot(data = priors2, aes(x = x1, y = a_den)) +
  geom_area(color = "black", fill = "grey30", alpha = 0.5) +
  scale_y_continuous(expand = expansion(mult = c(0.001, 0.05)), limits = c(0, max_dens_a_prior)) +
  annotate("text", x = 290, y = 0.095, label = "N(0, 4)", hjust = 1, color = "black", size = 3) +
  scale_x_continuous(expand = c(0, 0), breaks = c(-300, -150, 0, 150, 300)) +
  labs(
    y = "Density",
    x = expression(a[k]),
    subtitle = quote("Prior: Pr(" * a[1] * ")")
  )
f2.s2.panB <-
  ggplot(data = priors2, aes(x = x2, y = sigma_den)) +
  geom_area(color = "black", fill = "grey30", alpha = 0.5) +
  scale_y_continuous(expand = expansion(mult = c(0.01, 0.05))) +
  scale_x_continuous(expand = c(0, 0)) +
  annotate("text", x = 99, y = 0.045, label = "Exp(1/21)", hjust = 1, color = "black", size = 3) +
  labs(
    y = "Density",
    x = expression(sigma),
    subtitle = quote("Prior: Pr(" * sigma * ")")
  )
f2.s2.panD <-
  post_dens2 %>%
  ggplot(aes(x = x)) +
  geom_ribbon(aes(ymin = 0, ymax = y, fill = quant), alpha = 0.7) +
  geom_line(aes(y = y), color = "black") +
  labs(
    x = expression(a[1]),
    y = expression("Density"),
    subtitle = quote("Posterior: Pr(" * a[1] * " | y, x)")
  ) +
  scale_x_continuous(expand = c(0, 0), limits = range_a1) +
  scale_y_continuous(expand = expansion(mult = c(0.0, 0.05))) +
  scale_fill_manual(values = c("grey50", "grey70", "grey50")) +
  theme(legend.position = "None") +
  annotate("segment", x = 7, xend = 12, y = 0.02, yend = 0.05) +
  annotate("text", x = 11.5, y = 0.052, label = "90% Credible\ninterval", color = "black", size = 3, hjust = 0) +
  coord_flip(xlim = range_a1, ylim = c(0, max_dens))

layout <- "
ACCD
BCCD
"

fig2.s2 <- f2.s2.panA + f2.s2.panB + f2.s2.panC + f2.s2.panD +
  plot_layout(design = layout) +
  plot_annotation(tag_levels = "A")

fig2.s1


fig2.s2

Saving subfigures

save_fig(fig=fig2.s1, figname = "fig2-1", w = 6.2, h = 3.3)
save_fig(fig=fig2.s2, figname = "fig2-2", w = 6.2, h = 3.3)

8. Fig. 3: Priors vs Likelihood

8.1. Generate a larger sample

set.seed(999)
new_obs <- 150
x_fix2 <- rnorm(n = new_obs, 0, 1)
sample2 <- tibble(u = rnorm(new_obs, 0, 20), x = x_fix2, y = 1 + 2 * x_fix2 + u)
sample2 <- bind_rows(sample1, sample2)
n_obs2 <- new_obs + n_obs

input_data2 <- list(
  y = sample2$y,
  x = sample2$x,
  N = nrow(sample2)
)

8.2. Fitting the weakly informative model to larger sample

fit_wkinfo_priors_large <- model_wkinfo_priors$sample(
  data = input_data2,
  iter_sampling = 1000,
  iter_warmup = 1000,
  chains = 4,
  parallel_chains = 4,
  seed = 1234,
  refresh = 1000
)

Running MCMC with 4 parallel chains...

Chain 1 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 1 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 1 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 2 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 2 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 2 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 3 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 3 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 3 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 4 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 1 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 1 finished in 0.2 seconds.
Chain 2 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 2 finished in 0.1 seconds.
Chain 3 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 3 finished in 0.1 seconds.
Chain 4 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 4 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 4 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 4 finished in 0.1 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.3 seconds.
postdraws_wkinfo_prior_large <- fit_wkinfo_priors_large$draws(format = "draws_df")
fit_wkinfo_priors_large$summary(variables = c("sigma", "a0", "a1")) |> 
  mutate(across(where(is.numeric), round, 3))  |> 
  kable()
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
sigma 19.649 19.617 0.988 1.000 18.088 21.313 0.999 4670.806 2760.187
a0 -0.136 -0.149 1.383 1.358 -2.424 2.125 1.001 3777.942 2872.741
a1 2.467 2.467 1.324 1.337 0.317 4.634 1.000 3953.647 3027.360

8.3. Collecting Prior, likelihood, posterior for small, current sample

loglik_a1 <- function(a1, x, y, a0, u_sd) {
  resids <- y - (a0 + a1 * x)
  log_lik_vec <- dnorm(x = resids, mean = 0, sd = u_sd, log = TRUE)
  log_lik <- sum(log_lik_vec)
  return(log_lik)
}

ols_model_small <- lm(y ~ x, data = sample1)
a0 <- ols_model_small$coefficients[["(Intercept)"]]
usd <- sd(ols_model_small$residuals)
a1_hat <- ols_model_small$coefficients[["x"]]

small_sample_data <- tibble(a1 = seq(-20, +30, length.out = 1000))
small_sample_data$loglik <- map_dbl(
  small_sample_data$a1,
  loglik_a1,
  x = sample1$x,
  y = sample1$y,
  a0 = a0,
  u_sd = usd
)
small_sample_data <-
  small_sample_data %>%
  mutate(
    # norm_lik = -2 * loglik, #exp(loglik) / sum(exp(loglik)),
    norm_lik = (loglik),
    prior = dnorm(a1, 0, 4),
    post = approxfun(density(postdraws_wkinfo_prior$a1))(a1)
  ) 
small_sample_data$post[is.na(small_sample_data$post)] <- 0

8.4. Collecting Prior, likelihood, posterior for larger sample

ols_model_large <- lm(y ~ x, data = sample2)
a0 <- ols_model_large$coefficients[["(Intercept)"]]
usd <- sd(ols_model_large$residuals)
a1_hat_big <- ols_model_large$coefficients[["x"]]

large_sample_data <- tibble(a1 = seq(-20, +30, length.out = 1000))
large_sample_data$loglik <- map_dbl(
  large_sample_data$a1,
  loglik_a1,
  x = sample2$x,
  y = sample2$y,
  a0 = a0,
  u_sd = usd
)
large_sample_data <-
  large_sample_data %>%
  mutate(
    # norm_lik = -2 * loglik, #exp(loglik) / sum(exp(loglik)),
    norm_lik = (loglik),
    prior = dnorm(a1, 0, 4),
    post = approxfun(density(postdraws_wkinfo_prior_large$a1))(a1)
  ) 
large_sample_data$post[is.na(large_sample_data$post)] <- 0

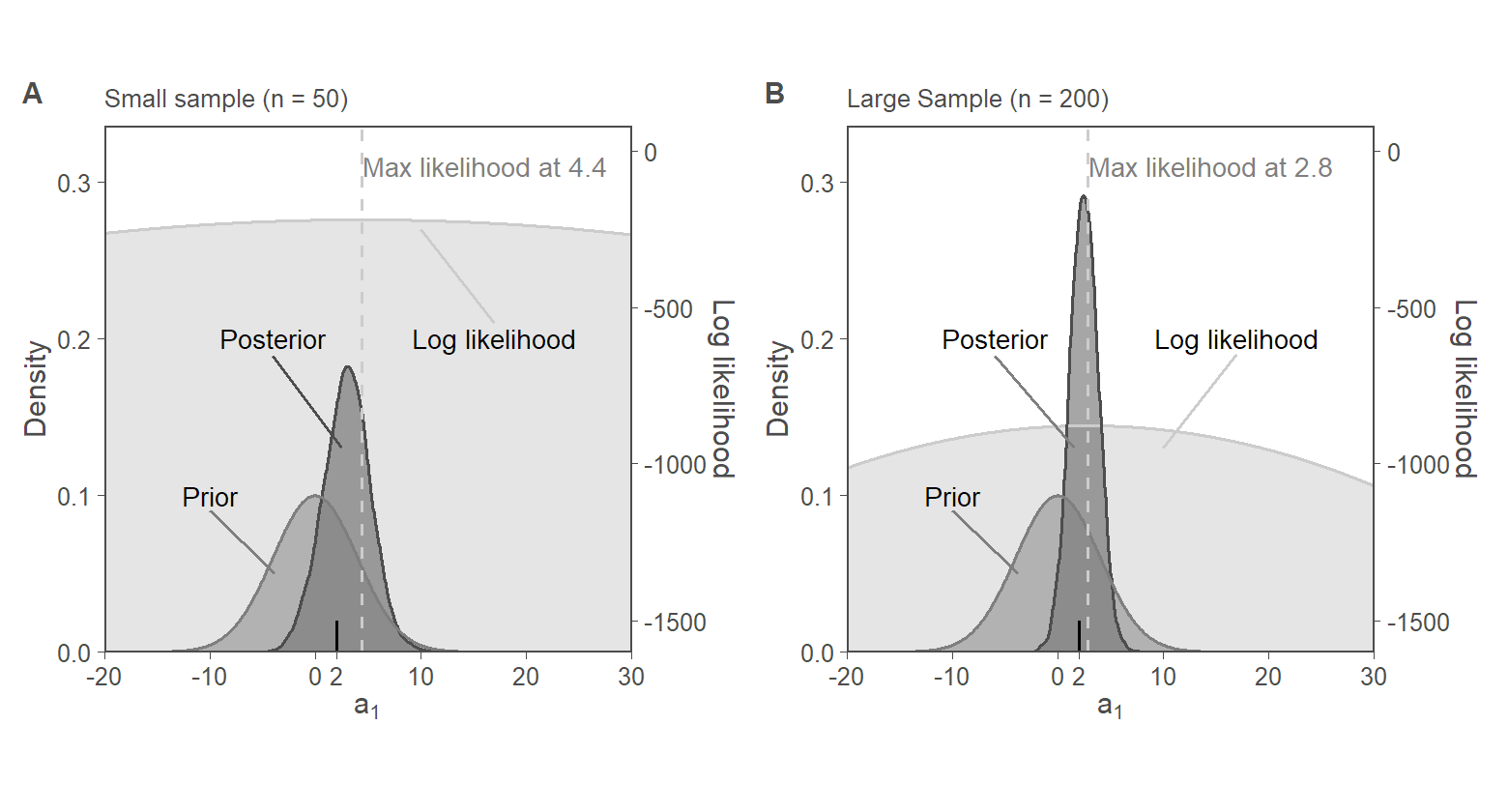
8.5. Fig. 3, Panel A and Panel B

SCALER_1 <- -2 * 0.0001
f3.panA <- 
  small_sample_data %>%
  mutate(norm_lik = (-1600 - norm_lik) * SCALER_1) %>%
  pivot_longer(c(norm_lik, prior, post), names_to = "part") %>%
  ggplot(aes(x = a1, y = value, group = part, color = part, fill = part)) +
  geom_ribbon(aes(ymin = 0, ymax = value), alpha = 0.5) +
  geom_line() + 
  geom_vline(xintercept = a1_hat, color = "grey80", linetype = "dashed") +
  labs(
    y = "Density",
    x = expression(a[1]),
    subtitle = "Small sample (n = 50)"
  ) +
  annotate("text",
    x = c(-10, -4, 17),
    y = c(0.1, 0.2, 0.20),
    label = c("Prior", "Posterior", "Log likelihood"),
    hjust = 0.5,
    size = 3
  ) +
  annotate("segment",
    x = c(-10, -4, 17),
    y = c(0.090, 0.189, 0.21),
    xend = c(-3.8, 2.5, 10),
    yend = c(0.050, 0.13, 0.27),
    color = c("grey50", "grey30", "grey80")
  ) +
  annotate("text",
    x = a1_hat + 0.1,
    y = 0.31, label = paste("Max likelihood at", round(a1_hat, 1)),
    hjust = 0, color = "grey50", size = 3
  )
  

f3.panB <- 
  large_sample_data %>%
  mutate(norm_lik = (-1600 - norm_lik) * SCALER_1) %>%
  pivot_longer(c(norm_lik, prior, post), names_to = "part") %>%
  ggplot(aes(x = a1, y = value, group = part, color = part, fill = part)) +
  geom_ribbon(aes(ymin = 0, ymax = value), alpha = 0.5) +
  geom_line() +
  geom_vline(xintercept = a1_hat_big, color = "grey80", linetype = "dashed") +
  labs(
    y = "Density",
    x = expression(a[1]),
    subtitle = "Large Sample (n = 200)"
  ) +
  annotate("text",
    x = c(-10, -6, 17),
    y = c(0.1, 0.2, 0.20),
    label = c("Prior", "Posterior", "Log likelihood"),
    hjust = 0.5,
    size = 3
  ) +
  annotate("segment",
    x = c(-10, -6, 17),
    y = c(0.090, 0.189, 0.19),
    xend = c(-3.8, 1.5, 10),
    yend = c(0.050, 0.13, 0.13),
    color = c("grey50", "grey50", "grey80")
  ) +
  annotate("text",
    x = a1_hat_big + .1,
    y = 0.31, label = paste("Max likelihood at", round(a1_hat_big, 1)),
    hjust = 0, color = "grey50", size = 3
  ) 

fig3 <- 
  f3.panA + f3.panB +
  plot_annotation(tag_levels = "A") &
  annotate("segment", x = 2, y = 0, xend = 2, yend = 0.02) &
  theme(legend.position = "none", aspect.ratio=1) & 
  scale_color_manual(values = c("grey80", "grey30", "grey50")) &
  scale_fill_manual(values = c("grey80", "grey30", "grey50")) &
  scale_y_continuous(
    expand = expansion(mult = c(0, 0.05)),
    limits = c(0, 0.32),
    sec.axis = sec_axis(~ -1600 - . / SCALER_1, name = "Log likelihood")
  ) &
  scale_x_continuous(
    breaks = c(-20, -10, 0, 2, 10, 20, 30),
    expand = expansion(mult = c(0, 0))
  )
fig3

Saving figure

save_fig(fig=fig3, figname = "fig3", w = 6.2, h = 3.1)

Corrections

If you see mistakes or want to suggest changes, please create an issue on the source repository.

Reuse

Text and figures are licensed under Creative Commons Attribution CC BY 4.0. Source code is available at https://github.com/hschuett/BayesForAccountingResearch, unless otherwise noted. The figures that have been reused from other sources don't fall under this license and can be recognized by a note in their caption: "Figure from ...".